---

5. Aufgabe (BM02x013)

Die nebenstehende Skizze zeigt eine Masse, die durch 3 Seilstücke (1, 2, 3) gehalten wird. Wie groß ist die Spannung im Seilstück 2? 19,6 N 33,9 N 0 N 17 N .......

 

---

6. Aufgabe (BM02x001)

Ein Stein wird mit der Anfangsgeschwindigkeit $ \overrightarrow{v_0} $ senkrecht nach oben geworfen. Angenommen werde eine Reibungskraft die proportional zu -$ \vec{v} $ ist ($ \vec{v} $ ist die Momentangeschwindigkeit des Steins). Kreuzen Sie alle richtigen Aussagen an!

Die Beschleunigung des Steins ist stets $ \vec{g} $.

Die Beschleunigung des Steins ist nur im höchsten Punkt gleich $ \vec{g} $.

Die Beschleunigung des Steins ist stets kleiner als $ \vec{g} $.

Der Stein kehrt mit der Geschwindigkeit $ v_0 $ an den Abwurfpunkt zurück.

Der Stein erreicht die Geschwindigkeit $ v_0 $ bereits wieder bevor er zum Ausgangspunkt zurückkehrt.

 

---

7. Aufgabe (BM02x003)

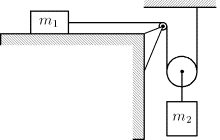
In der nebenstehenden Abbildung fällt die Masse $ m_2 $ gleichmäßig beschleunigt nach unten. Die Masse $ m_1 $ wird dadurch eben­falls beschleunigt. In welchem Verhältnis stehen die Beträge der Beschleunigungen $ a_1 $ und $ a_2 $ der Massen $ m_1 $ bzw. $ m_2 $, wenn man die Massen der Rollen und Seile sowie auch jede Reibung vernachlässigen kann.                                             $ \frac{a_1}{a_2}= $

 

---

8. Aufgabe (BM02x005)

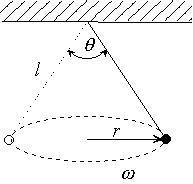
Die nebenstehende Abbildung zeigt eine Punktmasse m, die über einen Faden mit der festen Länge l an der Decke angebunden ist. Die Punktmasse bewegt sich mit konstanter Winkel­geschwindigkeit $ \omega $ auf einem horizontalen Kreis mit dem Radius r. Die Spannung im Faden ist dabei:

$ mg\left ( \frac{r}{l} \right ) $

$ mg\cdot \cos \left ( \frac{\theta}{2} \right ) $

$ \frac{m \omega r}{\sin \left ( \frac{\theta}{2} \right )} $

$ m \sqrt{\left ( \omega ^{2} r^{2} + g^{2}\right )} $

$ m \sqrt{\left ( \omega ^{4} r^{2} + g^{2}\right )} $

---

9. Aufgabe (BM02x008)

Sechs gleiche Würfel mit der Masse 1 kg liegen auf einem ebenen glatten Tisch. Eine konstante Kraft F = 1 N wirkt auf den ersten Würfel in Richtung des eingezeichneten Vektors. Geben sie die Größe der resultierenden Kraft F_i an, die jeweils auf einen Würfel wirkt. Welche Kraft F^* übt außerdem der Würfel 4 auf Würfel 5 aus?

---

10. Aufgabe (BM02x009)

Zwei gleiche Körper sind mit einem Faden verbunden und liegen auf einem ebenen glatten Tisch. Der Faden kann eine Kraft von maximal 20 N halten. Welche Kraft F ist mindestens auf den Körper 2 auszuüben, damit der Faden reißt?

 

 

Wie ändert sich das Ergebnis, wenn Reibung anzunehmen ist? (Für beide Körper soll der Reibungskoeffizient zur Tischplatte gleich groß sein.)

 

 

---

11. Aufgabe (BM02x010)

Ein Tennisspieler trifft beim Aufschlag den senkrecht nach oben geworfenen Ball genau im Umkehrpunkt und erteilt ihm eine Geschwindigkeit v = 200 km h^-1. Man nehme an, daß der Ball den Tennisschläger während eines Zeitintervalls Δt = 0,057 s berührt. Das Wieviel­fache der Erdbeschleunigung wirkt im Mittel während der Berührungszeit auf den Tennisball?

 

 

 

 

---

12. Aufgabe (BM02x012)

Eine Kette mit der Länge L und der Masse M hängt senkrecht über einer Platte. Das Ende der Kette berührt gerade die Oberfläche. Die Kette wird losgelassen und kann frei fallen. (Reibungskräfte zwischen den Kettengliedern und Effekte durch das Anhäufen der Kettenglieder am Boden werden vernachlässigt.) Wie groß ist die Kraft N, die durch die Kette auf die Platte ausgeübt wird, wenn das Kettenende ein Stück x (x < L) gefallen ist?

$ N=Mg-M\ddot{x} $

$ N=3Mg $

$ N=Mg-2M\ddot{x} $

$ N=\left ( \frac{3M}{L} \right )gx $

$ N=Mg $

---

13. Aufgabe (BM03x002)

Wo treten Trägheitskräfte auf, und welche Richtung haben sie?

 

 

---

14. Aufgabe (BM02x004)

In einer Aufzugskabine hängt an einer Federwaage ein Körper mit der Masse m = 10 kg. Die Federwaage zeigt eine Kraft von F = 115 N an. Welche der aufgeführten Bewegungsformen sind möglich? Bitte ankreuzen!

Gleichförmige Bewegung nach oben.
Gleichförmige Bewegung nach unten.
Gleichförmig beschleunigte, schneller werdende Bewegung nach oben.
Gleichförmig beschleunigte, schneller werdende Bewegung nach unten.
Gleichförmig beschleunigte, langsamer werdende Bewegung nach oben.
Gleichförmig beschleunigte, langsamer werdende Bewegung nach unten.

 

 

---

15. Aufgabe (BM03x001)

In welche Himmelsrichtung wird ein frei fallender Körper durch die Coriolis- bzw. Zentrifugalkraft abgelenkt, auf der

	Nördlichen Halbkugel	Südlichen Halbkugel
Corioliskraft:	N O S W	N O S W
Zentrifugalkraft:	N O S W	N O S W

 

---

 

16. Aufgabe (BM03x003)

In einer Aufzugskabine hängt an einer Federwaage ein Körper mit der Masse m = 10kg. Die Federwaage zeigt eine Kraft von F = 115 N an. Bewegt sich der Aufzug? Welche Fälle sind denkbar?

 

 

 

---

17. Aufgabe (BM03x004)

Geben Sie die horizontale Ablenkung eines Teilchens an, das im Schwerefeld der Erde frei fällt. Dabei soll l der Breitengrad und w die Winkelgeschwindigkeit der Erde sein.

$ \frac{1}{3}\omega \sqrt{\frac{8h^{3}}{g}} \cdot \cos \lambda $

$ 2\omega h \cdot \cos \lambda $

$ \omega \sqrt{8hg} \cdot \cos \lambda $

$ \omega R_E \sqrt{\frac{2h}{g}} \cdot \cos \lambda $

.......

 

---

18. Aufgabe (BM03x005)

Sie befinden sich in einer Aufzugskabine eines Hochhauses und fahren nach unten. Plötzlich tritt ein beängstigendes Geräusch auf. Ihr Nachbar lässt vor Schreck seine Aktentasche los, die aber nicht herunterfällt und einfach in der Luft stehen bleibt. Welchen Schluss müssen Sie daraus ziehen?

 

 

---

19. Aufgabe (BM02x015)

Betrachtet wird eine gleichmäßig beschleunigte Bewegung, die nicht aus der Ruhe startet, und bei der die Kraft in Wegrichtung wirkt. Benutzen Sie die Definition der Leistung als zeitliche Ableitung der Arbeit, um die Leistung in Abhängigkeit von der Zeit anzugeben. (Hinweis: Der Weg ist eine Funktion der Zeit!)

 

 

 

---

20. Aufgabe (BM02x014)

Ein Mann springt von einem Boot aus ans Ufer. (Das Boot liegt ruhig im Wasser, ist aber noch nicht festgebunden.) Verglichen mit einem Sprung gleicher Weite an Land muss er:

weniger

gleich viel

mehr

Energie aufbringen?

Begründung:

 

 

 

 

 

---