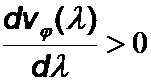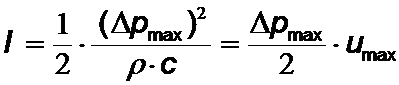Repetitorium zur Wellenlehre (R.Girwidz)
In der Physik gibt es übergeordnete Begriffe und Konzepte, die Phänomene aus verschiedenen Bereichen beschreiben und erklären können. Sie helfen, die Physik überschaubarer und verständlicher zu machen. Wellen sind dafür ein Beispiel. Kenntnisse aus einem Teilgebiet der Physik lassen sich in vielen Fällen gewinnbringend in andere übertragen.
Die folgende, knapp gehaltene Zusammenfassung orientiert sich zunächst an charakteristische Erscheinungen bei Wellen. Zugeordnet sind Definitionen, Formeln und Beispiele. Nach einem allgemeinen Teil folgen noch spezielle Hinweise zu Wasserwellen, elektromagnetischen Wellen (Dipolstrahlung) und zur Wellenoptik.
Zu den Kapiteln gibit es am Rand Hinweise, welche Programmteile den besprochenen Sachverhalt illustrieren können.
Das Programmpaket finden Sie unter "Download (alte Programme)". Die eindimensionale Wellenmaschine gibt es auch als Applet. Eine internetfähige Version des Repetitorium mit neuen Applets erscheint 2007.
Begriff der Welle
Eine vom Erreger fortschreitende Anregung heißt laufende Welle (noch allgemeiner: Betrachtet wird, wie sich physikalische Zustände von einem Ort aus durch den Raum ausbreiten).
Ein einfaches Modell in der Wellenlehre ist das Massepunkt-Federmodell: Angenommen werden Massenpunkte, die über masselose, elastische Federn gekoppelt sind. (Dieses Modell ist auch die Grundlage für verschiedene Computersimulationen.)
Eine harmonische Welle ist der Spezialfall eines räumlich und zeitlich periodischen, sinusförmigen Vorgangs. Im eindimensionalen Fall gilt dabei für die Auslenkungen s aus der Ruhelage:
oder:
mit der Phasengeschwindigkeit: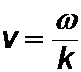 
Dabei gelten folgende Zusammenhänge zwischen Kreisfrequenz w, Frequenz f und Periodendauer T:
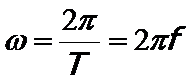
und zwischen Wellenzahl k und der Wellenlänge l:
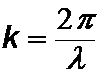
Menü: Wellenlänge
Die Phase gibt den momentanen Schwingungszustand eines Punktes an und wird durch den Phasenwinkel (hier Argument der Sinusfunktion) beschrieben. Die Wellenlänge ist dann der kürzeste Abstand zweier Punkte gleicher Phase.
Wellenarten
Bei Longitudinalwellen stimmen Ausbreitungs- und Schwingungsrichtung überein. Von Transversalwellen spricht man, wenn die Auslenkungen senkrecht zur Ausbreitungsrichtung erfolgen. Liegen dabei Elongation und Ausbreitungsrichtung stets in der gleichen Ebene, ist die Welle linear polarisiert. Wenn der Auslenkungsvektor (an einem Ort) mit konstanter Frequenz um die Ausbreitungsrichtung rotiert, heißt die Welle zirkular polarisiert.
Beispiele: Schallwellen sind Longitudinalwellen. Im Festkörper treten Longitudinal- und Transversalwellen auf. Elektromagnetische Wellen sind Transversalwellen.
Wellenphänomene
Prinzip der ungestörten Überlagerung und Superpositionsprinzip
Wellen können sich ohne gegenseitige Störung durchdringen (Prinzip der ungestörten Überlagerung). Dies gilt, wenn die Wellengleichung linear ist, bzw. wenn bei mechanischen Wellen ein lineares Kraftgesetz zugrunde gelegt werden kann. (Z.B. sind im Masse-Federmodell die Rückstellkräfte bei Störungen proportional zu den Auslenkungsunterschieden benachbarter Massen.) Die Elongation an der Überlagerungsstelle erhält man, indem man die Auslenkungen der Einzelwellen vektoriell addiert (Superpositionsprinzip).
Menü: Superposition
Die Superponierbarkeit ist grundlegend für das Verständnis von Interferenzversuchen und für das Huygenssche Prinzip. Außerdem ist dies auch eine notwendige Voraussetzung dafür, daß jede Wellenform als Überlagerung einfacher harmonischer Wellen verstanden werden kann.
Huygenssches Prinzip
Nach dem Huygensschen Prinzip kann jeder Punkt, der von einer Welle erfaßt wird, selbst als Zentrum einer Elementarwelle betrachtet werden. Die registrierbare Wellenfront ist jeweils die Einhüllende der Wellenfronten aller Elementarwellen. (Somit ist die ungestörte Überlagerung vorausgesetzt.)
Menü: Elementarwellen
Beugung und Interferenz
Als Beugung bezeichnet man die Abweichung von der geradlinigen Ausbreitung einer Welle an den Grenzen eines Hindernisses.
Interferenz steht für die Gesamtheit der Überlagerungserscheinungen beim Zusammentreffen von Wellenzügen mit festen Phasenbeziehungen (kohärente Wellen).
Menü: Doppelspalt
Nach Crawford (1989) nennt man aus historischen Gründen das Muster, das aus einer Überlagerung der Beiträge einer "kontinuierlichen" Verteilung kohärenter Quellen entsteht ein Beugungsmuster (z.B. Beugung an einer Kante). Betrachtet man eine endliche Zahl diskreter kohärenter Quellen, spricht man von Interferenzmustern.
Das Verhalten von Wellen am Doppelspalt läßt sich über Interferenzbetrachtungen leicht verstehen. Für das Maximum k-ter Ordnung gilt:
:
(a ist der Spaltabstand, l die Wellenlänge. ak sind die Winkel, unter denen die Maxima erscheinen.)
Energietransport ohne Materialtransport
Fortschreitende Welle transportieren Energie, ohne daß dies an einen Materialtransport gebunden ist. Materieteilchen werden, sofern überhaupt beteiligt, nur um einen mittleren Ruhepunkt bewegt. Bei mechanischen Wellen findet ein fortlaufender Wechsel zwischen potentieller und kinetischer Energie statt. Die mittlere Energiedichte einer fortschreitenden elastischen Welle ist proportional zum Quadrat ihrer Amplitude und dem Quadrat der Frequenz:
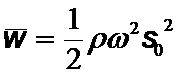
Aus Energiebetrachtungen ist auch ableitbar, daß die Amplitude
ebener harmonischer Wellen ohne Reibungsverluste konstant bleibt, jedoch bei
Kreis- / Zylinderwellen mit 
und bei Kugelwellen mit 
abnimmt.
Die Intensität I (oder mittlere Energiestromdichte) einer Welle ist definiert als Energie, die pro Zeiteinheit durch die Flächeneinheit senkrecht zur Fortpflanzungsrichtung strömt. Sie ist das zeitliche Mittel der momentanen Energieflußdichte S:
( c: Ausbreitungsgeschwindigkeit; 
mittleren Energie pro Volumen.)
In Raumbereichen ohne Erreger gilt natürlich die Kontinuitätsgleichung:
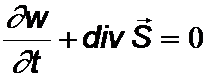
Phasen- und Gruppengeschwindigkeit, Dispersion
Menü: Dispersion
In Materie ist die Ausbreitungsgeschwindigkeit einer Störung abhängig vom Medium und genau betrachtet i.a. auch von der Form der Störung. Die Phasengeschwindigkeit vj ist die Ausbreitungsgeschwindigkeit einer harmonischen bzw. sinusförmigen Welle. Die Gruppengeschwindigkeit vG beschreibt die Ausbreitung einer impulsartigen Störung bzw. einer Wellengruppe. (Diese läßt sich als Überlagerung harmonischer Wellen unterschiedlicher Frequenz auffassen.) Die Gruppengeschwindigkeit gibt auch an, wie schnell ein Signal bzw. Energie durch eine Welle übertragen wird. So ist die Lichtgeschwindigkeit im Vakuum eine obere Grenze für vG .
Ist die Phasengeschwindigkeit von der Wellenlänge abhängig, so spricht man von Wellen mit Dispersion, und zwar
| von normaler Dispersion für
|
("große Wellenlängen |
von anormaler Dispersion für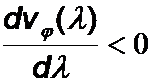 
.
Die Dispersionsrelation, d.h. die Funktion w(k) kennzeichnet die dispersiven Eigenschaften eines Mediums. Aus ihr sind auch Gruppen- und Phasengeschwindigkeit zu entnehmen:
; 
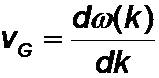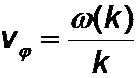
In der Beziehung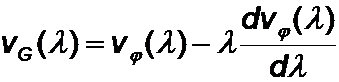 
wird deutlich: vG < vj für normale Dispersion
vG > vj für anormale Dispersion.
Anm: Bei mechanischen Wellen ist die Teilchengeschwindigkeit, die Schnelle u, grundsätzlich von der Gruppen- und der Phasengeschwindigkeit zu unterscheiden.
Die lineare Kette ist ein gutes Beispiel für einen Wellenträger mit Dispersion. Die Dispersionsrelation lautet:
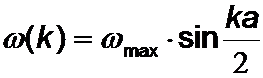mit: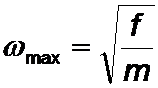 
a ist der Abstand zwischen den Massen m; f ist anschaulich die Federhärte der masselosen Kopplungsfedern.
Reflexionen
Menü:
Reflexion1
Reflexion2
Zwei Medien
Treffen Wellen auf Begrenzungen, über die sie sich nicht ausbreiten können, werden sie reflektiert (z.B. Licht an einem Spiegel, Schall an einer Felswand). Dabei ist zwischen einer Reflexion am "festen Ende" und einer Reflexion am "offenen / losen Ende" zu unterscheiden.
Reflexion am festen Ende:
Transversalwelle: Die Richtung der Auslenkung wird umgekehrt; Phasensprung p bei harmonischen Wellen; Knoten der Auslenkung am Ende.
Longitudinalwelle: Verdichtung wird als Verdichtung, Verdünnung als Verdünnung reflektiert. Eine reflektierte Wechseldruckwelle ändert am festen Ende die Phase nicht; Druckbauch am Ende.
Reflexionen am offenen / losen Ende:
Transversalwellen: Bei der Reflexion einer Querwelle am losen Ende bleibt die Richtung der Auslenkung erhalten; kein Phasensprung bei einer harmonischen Welle; Auslenkungsbauch am losen Ende.
Longitudinalwellen: Bei der Reflexion einer Längswelle wird Verdichtung als Verdünnung reflektiert und umgekehrt. Bei harmonischen Wechseldruckschwingungen ändert sich die Phase sprunghaft um p.
Der Wellenwiderstand (bei mechanischen Wellen)
Welche Kraft ist aufzubringen, um eine Welle anzuregen, die von einem Seilende aus fortschreitet?
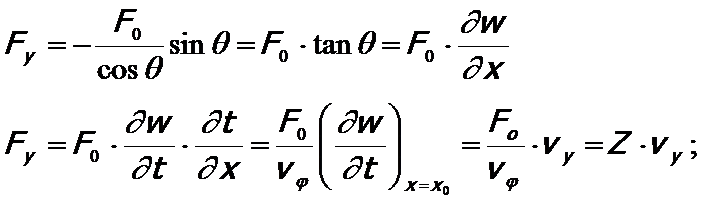
Die Kraft Fy ist proportional zur zeitlichen Änderung der Auslenkung und formal vergleichbar mit der Reibungskraft bei einer gedämpften Schwingung (Fy~vy). Der Poportionalitätsfaktor ist der Wellenwiderstand bzw. die Wellenimpedanz Z.
Für Seilwellen gilt:
Anm.: Reflexionfreie Wellen / eine unendliche Wellenausbreitung läßt sich simulieren, wenn man ein Medium mit seinem Wellenwiderstand abschließt.
Transmission und Reflexion
Menü:
Zwei Medien
Zwei Medien 1
Zwei Medien 2
Läuft eine Welle in ein anderes Medium, ändert sich die Wellenlänge. Stets wird zumindest ein Teil der Welle reflektiert. (Anm: Dies gilt ebenso im zweidimensionalen Fall, auch wenn der Grenzwinkel der Totalreflexion noch nicht überschritten ist.)
Interessant ist, als Beispiel die Amplitude von reflektierter und transmittierter Welle (AT und AR) auf einem Seil zu betrachten, das aus zwei unterschiedlichen Stücken zusammengesetzt ist.
; 
.
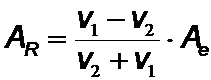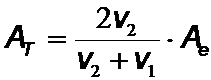AT ist stets positiv, und die durchlaufende Welle hat das gleiche Vorzeichen wie die einfallende Welle. Für den reflektierten Anteil sind jedoch zwei Fälle zu unterscheiden: Läuft die Welle vom Medium mit der kleineren Ausbreitungsgeschwindigkeit (z.B. schwächerer Kopplung der Kettenglieder bei gleicher Masse) in ein Medium mit größerer Ausbreitungsgeschwindigkeit, so hat die reflektierte Amplitude das umgekehrte Vorzeichen, die reflektierte Welle macht einen Phasensprung. Im anderen Fall bleibt das Vorzeichen gleich.
Für elektromagnetische Wellen gilt entsprechend den Fresnelschen Formeln speziell für den senkrechen Einfall:
; 
.
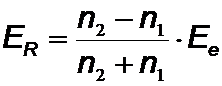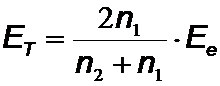Stehende Wellen
Menü: Stehende Wellen
(Eindimensionale) stehende Wellen können verstanden werden als Überlagerung von (zwei) Wellen gleicher Amplitude und Frequenz, aber entgegengesetzter Laufrichtung. Charakteristisch sind ortsfeste Knoten / Bäuche, jeweils im Abstand einer halben Wellenlänge. In der mathematischen Beschreibung sind Orts- und Zeitabhängigkeit separierbar (hier für eindimensionale stehende Wellen).
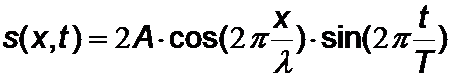
Stehende Wellen sind nur bei bestimmten Frequenzen, den Eigenfrequenzen eines Systems möglich. Sie sind durch die Randbedingungen des Mediums bzw. der räumlichen Struktur festgelegt. Eigenschwingungen / Eingenfrequenzen spielen in der Akustik, aber auch in der Modernen Physik (insbesondere Quantenmechanik, Festkörperphysik) eine wichtige Rolle.
Brechung
Menü: Zwei Medien
Beim Übergang von Wellen in ein zweites Medium ändert sich die Wellenlänge:
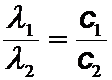
Beim schrägen Einfall auf die Genzfläche werden der Wellenstahlen (Senkrechte zur Wellenfront) gebrochen bzw. der Wellenvektor nach dem Brechungsgesetz von Snellius geändert
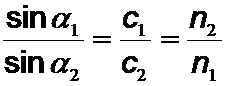
(Die Winkel werden zum Lot hin gemessen.
n1, n2 sind die jeweiligen Brechungsindizes.)
Die Wellengleichung, allgemeine Darstellung von Wellen
Die d'Alembertsche Wellengleichung beschreibt die ungestörte Ausbreitung von Wellen.
Im eindimensionalen Fall:
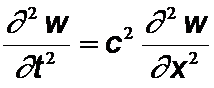
Allgemein:
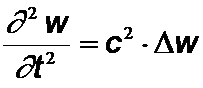
(D ist der Laplace-Operator)
Beispiele:
Wellengleichung für kompressible Medien:
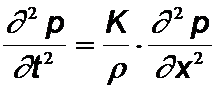
bzw. allg.:
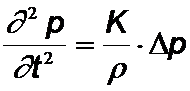
K ist der Kompressionsmodul (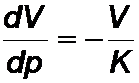 
) , r die Dichte.
Die Schallgeschwindigkeit in Gasen erhält man, wenn man den
isentropen Kompressionsmodul idealer Gase für K einsetzt, d.h.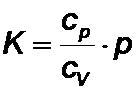 
. Aus dem Vergleich mit der Wellengleichung erkennt man sofort den Ausdruck
für die Schallgeschwindigkeit:
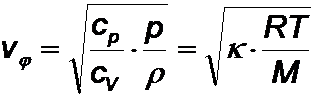
(M: molare Masse; k: Isentropen- / Adiabatenexponent)
Seilwellen:
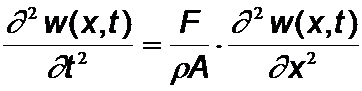
Dabei ist das Seil vom Querschnitt A und der Dichte r mit der Kraft F gespannt.
Elektromagnetische Wellen im Vakuum:
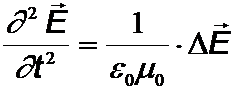
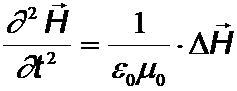
Dopplereffekt
Der normale Dopplereffekt tritt bei bewegtem Sender und / oder bewegtem Empfänger und Wellen auf, die an ein Medium gebunden sind (z.B. bei Schallwellen). Elektromagnetische Wellen zeigen demgegenüber den relativistischen Dopplereffekt.
Menü: Dopplereffekt
Frequenz- und Wellenlängenverschiebung bei bewegtem Sender (und Empfänger) lassen sich leicht aus einer Betrachtung der Wellenfronten herleiten (siehe Skizze).
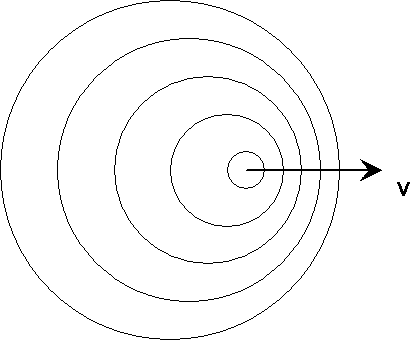
Bewegen sich Sender und Empfänger auf der x-Achse, so gilt
* bei bewegtem Beobachter (Sender ruht):
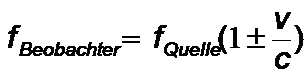
* bei bewegtem Sender (Beobachter ruht):
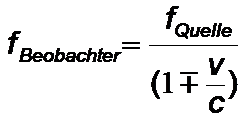
oder allgemein:
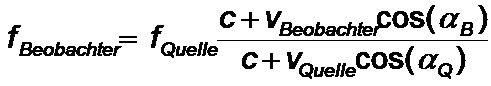
Der relativistische Dopplereffekt
Entscheidend ist nur die Relativgeschwindigkeit zwischen Quelle und Beobachter. (Die Lichtgeschwindigkeit ist für jedes Bezugssystem konstant.)
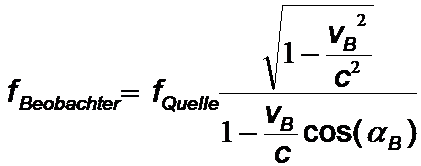
Wellen auf Flüssigkeitsoberflächen
Menü: Wasserwellen
Wasserwellen sind nicht durch ein einfaches Massen-Federmodell zu beschreiben. Oberflächenwellen sind durch Dichte r, Oberflächenspannung s und die Tiefe h der Flüssigkeit beeinflußt.
Schwerewellen, d.h. Wellen bei denen der Einfluß der Oberflächenspannung vernachlässigbar ist, zeigen auf untiefen Flüssigkeiten (l << h) zeigen keine Dispersion, auf tiefen Flüssigkeiten (l >> h) normale Dispersion. Oberflächenwellen sehr kleiner Wellenlängen sind entscheidend durch die Oberflächenspannung der Flüssigkeit geprägt. Sie zeigen anormale Dispersion.
