Wellenphänomene

Prinzip der ungestörten Überlagerung und Superpositionsprinzip

Wellen können sich ohne gegenseitige Störung durchdringen (Prinzip der ungestörten Überlagerung). Dies gilt, wenn die Wellengleichung linear ist, bzw. wenn bei mechanischen Wellen ein lineares Kraftgesetz zugrunde gelegt werden kann. (Z.B. sind im Masse-Federmodell die Rückstellkräfte bei Störungen proportional zu den Auslenkungsunterschieden benachbarter Massen.) Die Elongation an der Überlagerungsstelle erhält man, indem man die Auslenkungen der Einzelwellen vektoriell addiert (Superpositionsprinzip).

Menü: Superposition

Die Superponierbarkeit ist grundlegend für das Verständnis von Interferenzversuchen und für das Huygenssche Prinzip. Außerdem ist dies auch eine notwendige Voraussetzung dafür, daß jede Wellenform als Überlagerung einfacher harmonischer Wellen verstanden werden kann.

Huygenssches Prinzip

Nach dem Huygensschen Prinzip kann jeder Punkt, der von einer Welle erfaßt wird, selbst als Zentrum einer Elementarwelle betrachtet werden. Die registrierbare Wellenfront ist jeweils die Einhüllende der Wellenfronten aller Elementarwellen. (Somit ist die ungestörte Überlagerung vorausgesetzt.)

Menü: Elementarwellen

Beugung und Interferenz

Als Beugung bezeichnet man die Abweichung von der geradlinigen Ausbreitung einer Welle an den Grenzen eines Hindernisses.

Interferenz steht für die Gesamtheit der Überlagerungserscheinungen beim Zusammen­treffen von Wellenzügen mit festen Phasenbeziehungen (kohärente Wellen).

Menü: Doppelspalt

Nach Crawford (1989) nennt man aus historischen Gründen das Muster, das aus einer Überlagerung der Beiträge einer "kontinuierlichen" Verteilung kohärenter Quellen entsteht ein Beugungsmuster (z.B. Beugung an einer Kante). Betrachtet man eine endliche Zahl diskreter kohärenter Quellen, spricht man von Interferenzmustern.

Das Verhalten von Wellen am Doppelspalt läßt sich über Interferenz­betrachtungen leicht verstehen. Für das Maximum k-ter Ordnung gilt:          

              :

(a ist der Spaltabstand, l die Wellenlänge. a_k  sind die Winkel, unter denen die Maxima erscheinen.)

 

 

---

 

Reflexionen

Menü:
Reflexion1
Reflexion2
Zwei Medien

Treffen Wellen auf Begrenzungen, über die sie sich nicht ausbreiten können, werden sie reflektiert (z.B. Licht an einem Spiegel, Schall an einer Felswand). Dabei ist zwischen einer Reflexion am "festen Ende" und einer Reflexion am "offenen / losen Ende" zu unterscheiden.

Reflexion am festen Ende:

        Transversalwelle: Die Richtung der Auslenkung wird umgekehrt; Phasen­sprung p bei harmonischen Wellen; Knoten der Auslenkung am Ende.

        Longitudinalwelle: Verdichtung wird als Verdichtung, Verdünnung als Verdünnung reflektiert. Eine reflektierte Wechseldruckwelle ändert am festen Ende die Phase nicht; Druckbauch am Ende.

Reflexionen am offenen / losen Ende:

        Transversalwellen: Bei der Reflexion einer Querwelle am losen Ende bleibt die Richtung der Auslenkung erhalten; kein Phasensprung bei einer harmonischen Welle; Auslenkungsbauch am losen Ende.

        Longitudinalwellen: Bei der Reflexion einer Längswelle wird Verdichtung als Verdünnung reflektiert und umgekehrt. Bei harmonischen Wechsel­druck­schwingungen ändert sich die Phase sprunghaft um p.

 

 

---

 

Transmission und Reflexion

Menü:
Zwei Medien
Zwei Medien 1
Zwei Medien 2

Läuft eine Welle in ein anderes Medium, ändert sich die Wellenlänge. Stets wird zumindest ein Teil der Welle reflektiert. (Anm: Dies gilt ebenso im zweidimensionalen Fall, auch wenn der Grenzwinkel der Totalreflexion noch nicht überschritten ist.)

Interessant ist, als Beispiel die Amplitude von reflektierter und transmittierter Welle (A_T und A_R) auf einem Seil zu betrachten, das aus zwei unterschiedlichen Stücken zusammengesetzt ist.

   ;                .

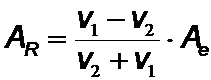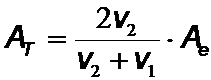A_T ist stets positiv, und die durchlaufende Welle hat das gleiche Vorzeichen wie die einfallende Welle. Für den reflektierten Anteil sind jedoch zwei Fälle zu unterscheiden: Läuft die Welle vom Medium mit der kleineren Ausbreitungs­geschwindigkeit (z.B. schwächerer Kopplung der Kettenglieder bei gleicher Masse) in ein Medium mit größerer Ausbreitungsgeschwindigkeit, so hat die reflektierte Amplitude das umgekehrte Vorzeichen, die reflektierte Welle macht einen Phasensprung. Im anderen Fall bleibt das Vorzeichen gleich.

Für elektromagnetische Wellen gilt entsprechend den Fresnelschen Formeln speziell für den senkrechen Einfall:

   ;             .

 

 

---

 

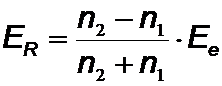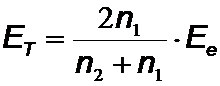Brechung

Menü: Zwei Medien

Beim Übergang von Wellen in ein zweites Medium ändert sich die Wellenlänge:

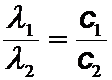
Beim schrägen Einfall auf die Genzfläche werden der Wellenstahlen (Senk­rechte zur Wellenfront) gebrochen bzw. der Wellenvektor nach dem Brechungs­gesetz von Snellius geändert

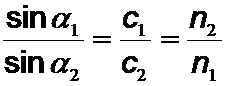
(Die Winkel werden zum Lot hin gemessen.

n₁, n₂ sind die jeweiligen Brechungsindizes.)

 

 

---

Dopplereffekt

Der normale Dopplereffekt tritt bei bewegtem Sender und / oder bewegtem Empfänger und Wellen auf, die an ein Medium gebunden sind (z.B. bei Schallwellen). Elektromagnetische Wellen zeigen demgegenüber den relativistischen Dopplereffekt.

Menü: Dopplereffekt

Frequenz- und Wellenlängenverschiebung bei bewegtem Sender (und Empfänger) lassen sich leicht aus einer Betrachtung der Wellenfronten herleiten (siehe Skizze).

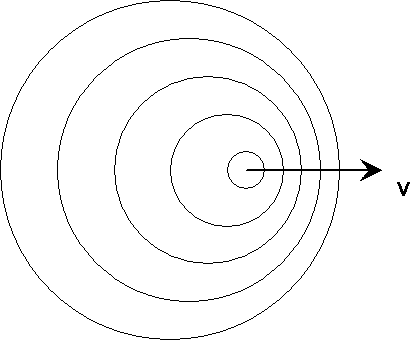
Bewegen sich Sender und Empfänger auf der x-Achse, so gilt

*   bei bewegtem Beobachter (Sender ruht):

                       

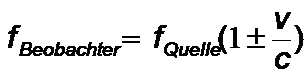
*   bei bewegtem Sender (Beobachter ruht):

                       

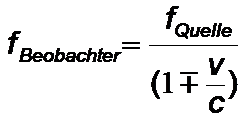
oder allgemein:          

                                              

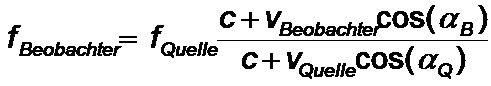
Der relativistische Dopplereffekt

Entscheidend ist nur die Relativgeschwindigkeit zwischen Quelle und Beobachter. (Die Lichtgeschwindigkeit ist für jedes Bezugssystem konstant.)